/ DATA

합성곱 신경망 기초 2(CNN, 역전파 Backpropagation)

CNN 강좌는 여러 절로 구성되어 있습니다.

CNN foward pass

1

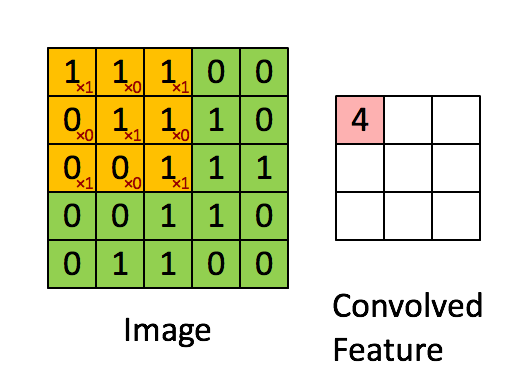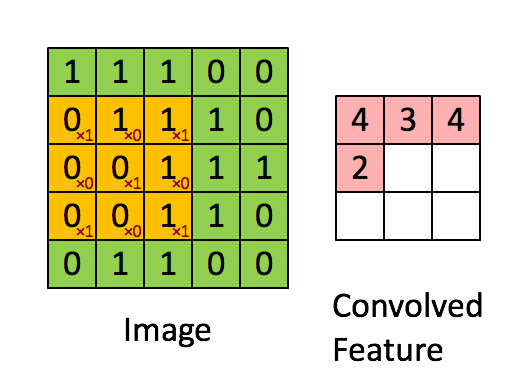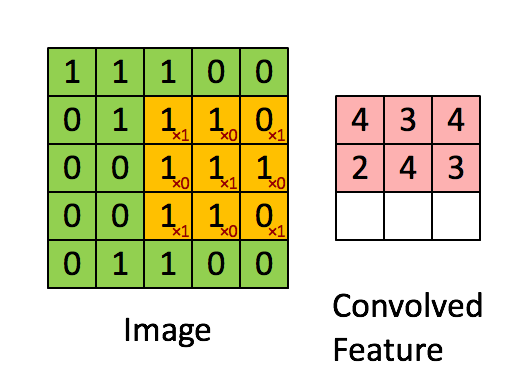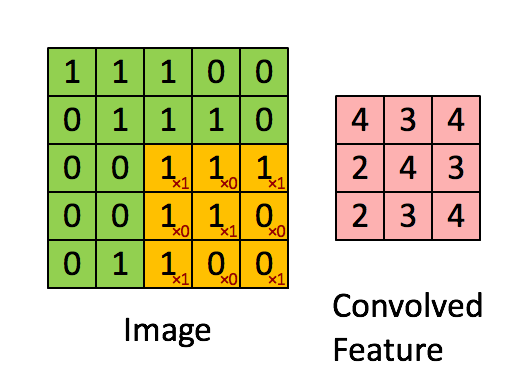
  • CNN은 필터가 입력데이터를 슬라이딩하면서 지역적 특징(feature)을 추출
  • 이 특징을 최대값(Max Pooling)이나 평균값(Average Pooling)으로 압축해 다음 레이어로 전달
  • 이런 과정을 반복해 분류 등 원하는 결과를 만들어내는 것이 CNN의 일반적인 구조

[Cross-Correlation] 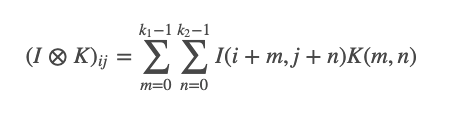1_2 [Convolution] 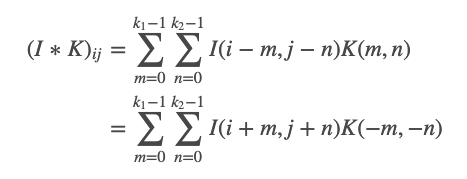1_1 K(−m,−n) == K(m,n)일 때, Convolution 과 Cross-Correlation이 동일하다.

3

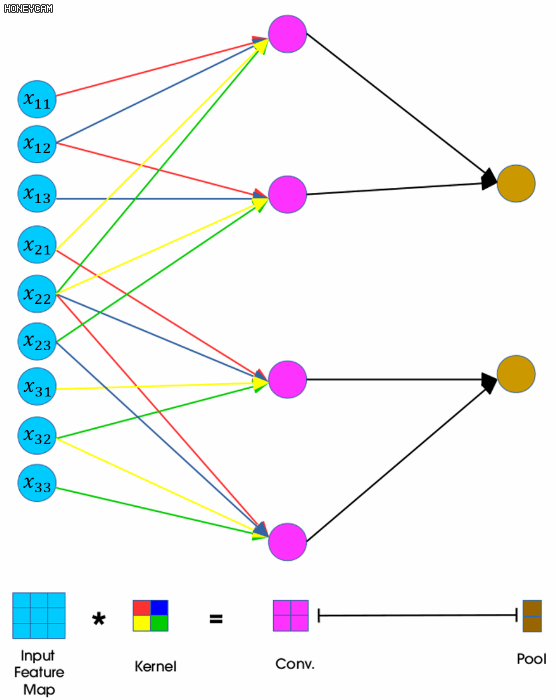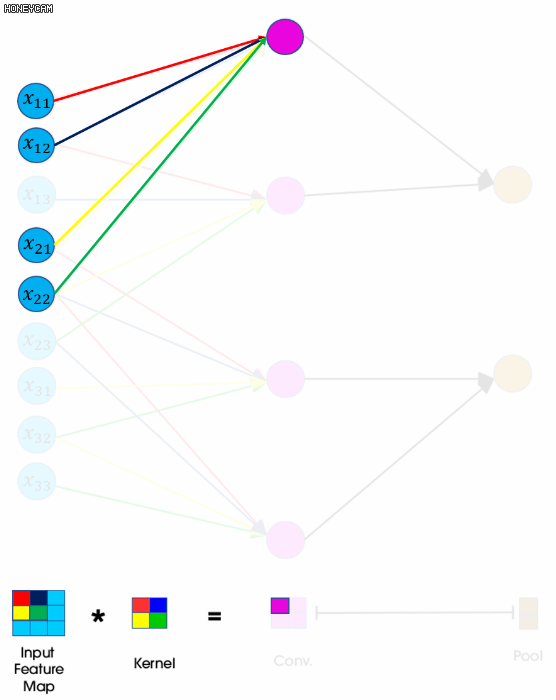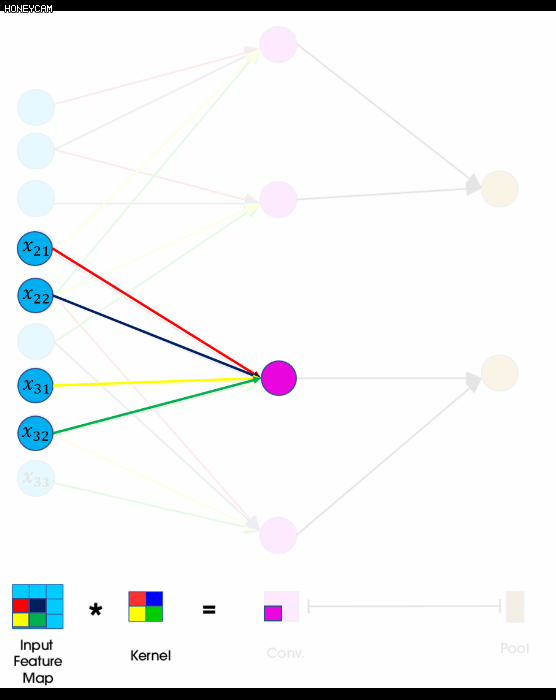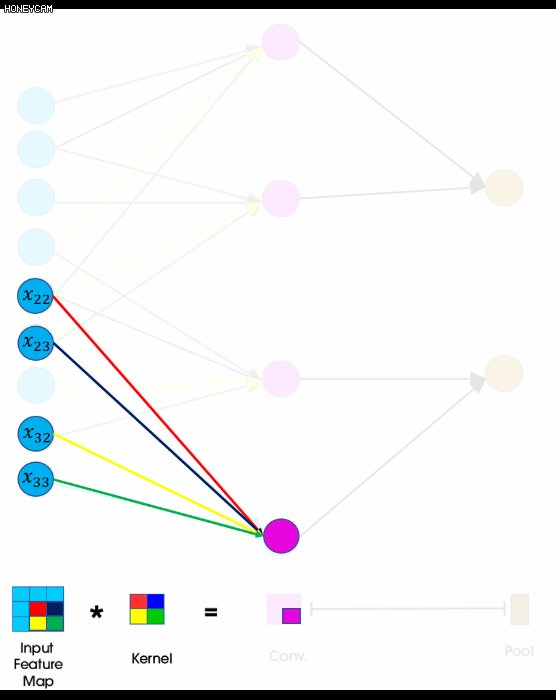
  • 𝑥𝑖𝑗 는 각각 입력값의 𝑖번째 행, 𝑗번째 열의 요소
  • 3x3 행렬, 2x2 필터(커널), 스트라이드 1
  • 이후 conv 레이어에 최대값이나 평균값을 취해서 정보를 압축(pooling)되어 2x2 행렬이 2x1 벡터로 바뀐다.

CNN backward pass

[Average Pooling 레이어의 그래디언트 전파 과정]

  • CNN 역전파 공식 (가중치 변화에 따른 오차 변화량)
  • HxW feature Map, k1 x k2 kernel 일 때, output은 (H-k1+1),(W-k2+1)

eq_1 eq_2

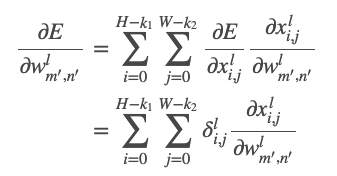
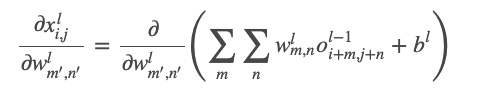
  • 현재 지점(x)의 그래디언트 식 eq_3
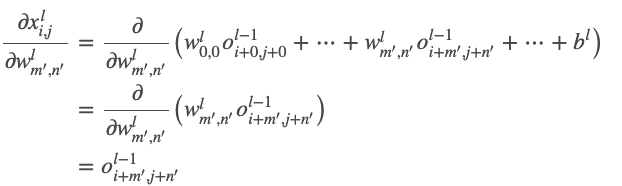
  • 최종 식 eq_4

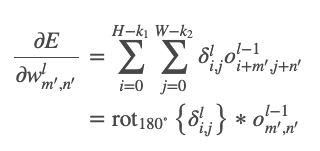
[Average Pooling] 4

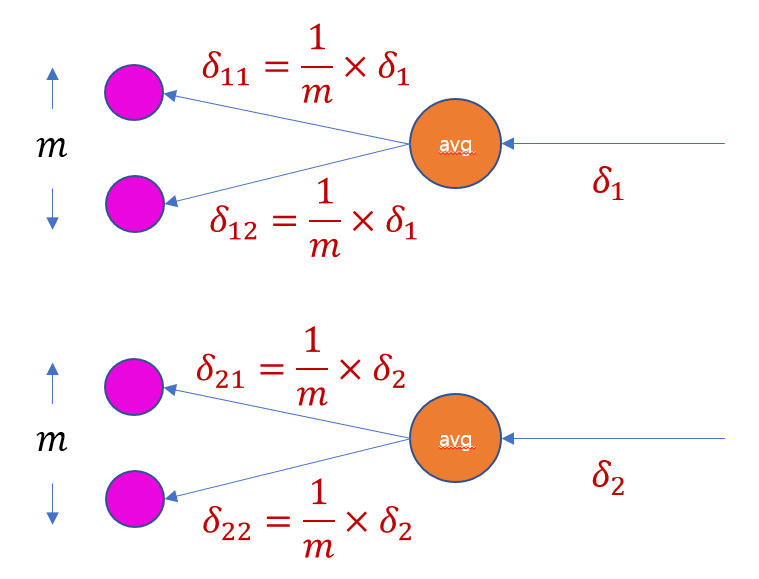
  • 바로 뒤 레이어로부터 전파된 그래디언트가 𝑑1, 𝑑2
  • 현재 지점의 그래디언트는 미분의 연쇄법칙(chain rule)에 의해 흘러들어온 그래디언트(d)에 로컬 그래디언트(w 혹은 x)를 곱한 것과 같음
  • Average Pooling을 하는 지점의 로컬 그래디언트는 1/𝑚

[Max Pooling] 5

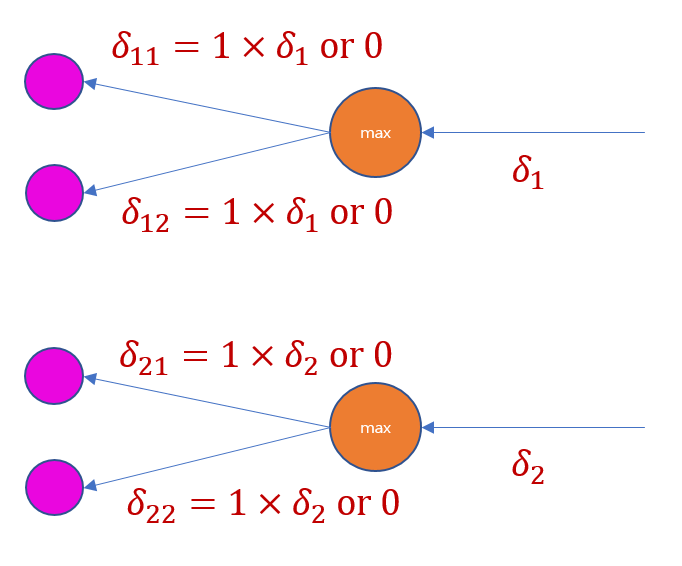
  • 가장 큰 값이 속해 있는 요소의 로컬 그래디언트는 1, 나머지는 0

[Convolution Layer] 6

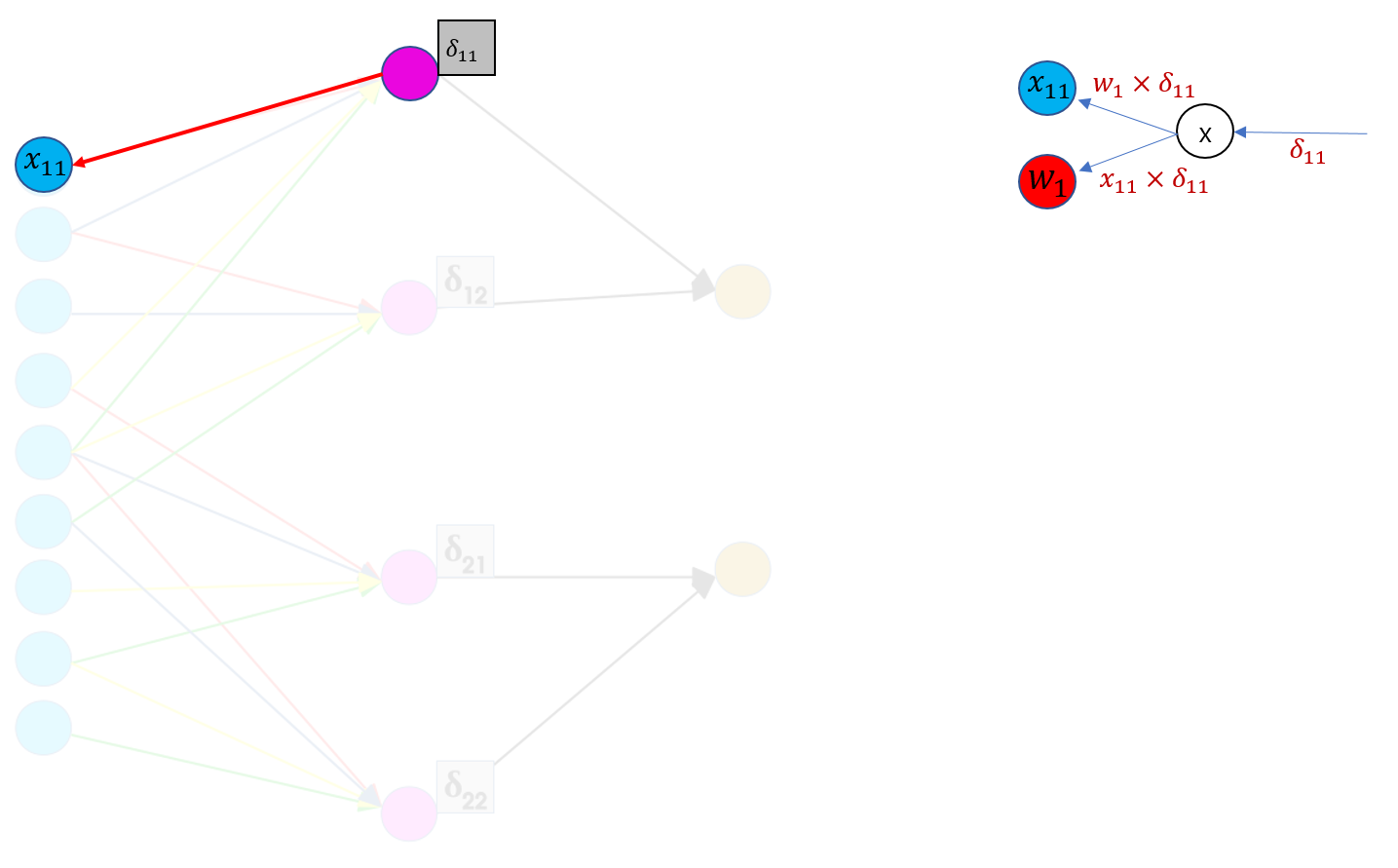
  • 𝑥11 은 forward pass 과정에서 2x2필터 가운데 빨간색(𝑤1) 가중치하고만 합성곱이 수행 되므로 역전파 때도 마찬가지로 딱 한번의 역전파가 일어남
  • Kapathy의 계산그래프 형태로 나타내면 𝑥11 의 그래디언트는 흘러들어온 그래디언트 𝑑11에 로컬 그래디언트(𝑤1)를 곱해서 구할 수 있다.
  • 마찬가지로 𝑤1 의 그래디언트는 흘러들어온 그래디언트 𝑑11에 로컬 그래디언트(𝑥11)를 곱해 계산

7

  • 하지만 이렇게 하나하나 따져가면서 구하려면 식이 복잡하고 이해가 어렵다.
  • conv layer가 역전파를 할 때 약간의 트릭을 쓰면 조금 더 간단히 그래디언트를 구할 수 있다.

간단한 방법 5_1 8

  • 흘러들어온 그래디언트 행렬에(2x2 크기)을 conv layer를 만들 때 썼던 필터가 슬라이딩하면서 값을 구한다
  • 필터 요소의 순서를 정반대로 바꿔 예컨대 빨-파-노-초 필터를 초-노-파-빨 필터로 바꿔서 그래디언트 행렬에 합성곱을 수행해주면 입력벡터(x)에 대한 그래디언트를 구할 수 있다.
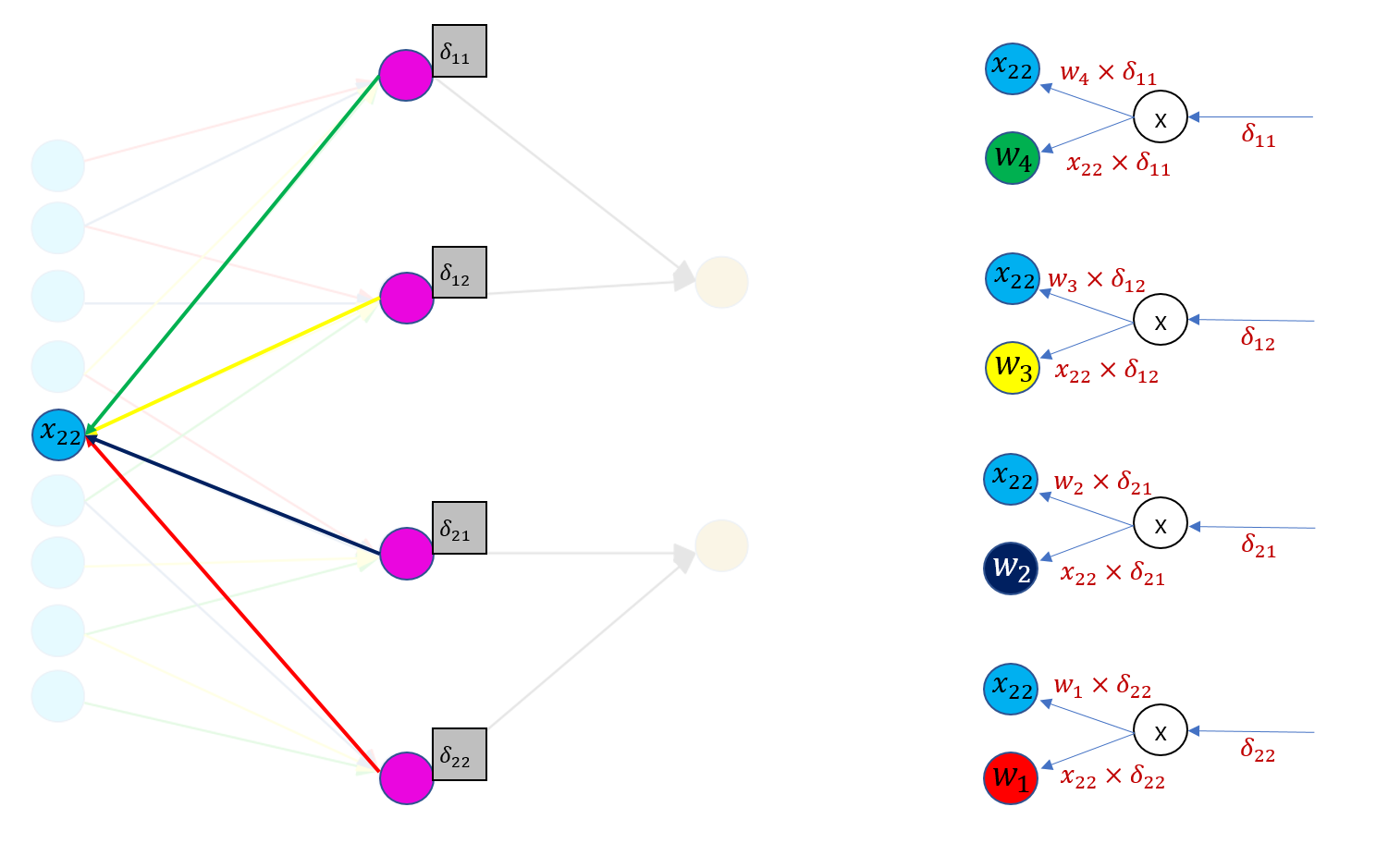
  • 필터의 그래디언트는 그래디언트 행렬 첫번째 요소인 𝑑11은 𝑥11, 𝑥12, 𝑥21, 𝑥22와 연결되어 있는 걸 확인할 수 있다. (영향을 끼치는 곳) 흘러들어온 그래디언트(𝑑11, 𝑑12, 𝑑21, 𝑑22)에 로컬 그래디언트(x11, x12, x21, x22)를 곱한다.
  • 각각의 로컬 그래다언트는 합성곱 필터 가중치로 연결된 입력값들이기 때문에 𝑑𝑤11은 𝑥11𝑑11+𝑥12𝑑12+𝑥21𝑑21+𝑥22𝑑22

참조 문헌

https://cs231n.github.io/optimization-2/
https://www.jefkine.com/general/2016/09/05/backpropagation-in-convolutional-neural-networks/
https://ratsgo.github.io/deep%20learning/2017/04/05/CNNbackprop/