합성곱 신경망 기초 6(ResNet, Residual Learning for Image Recognition)
CNN 강좌는 여러 절로 구성되어 있습니다.
- 합성곱 신경망 기초(CNN, Convolution Neural Network)
- 합성곱 신경망 기초 2(역전파, Backpropagation)
- 합성곱 신경망 기초 3(배치정규화, Batch Normalization)
- 합성곱 신경망 기초 4(가중치 초기화, Weight Initialization)
- 합성곱 신경망 기초 5(VGGNet, Very Deep Convolutional Network)
- 합성곱 신경망 기초 6(ResNet, Residual Learning for Image Recognition)
- 합성곱 신경망 기초 7(EfficientNet, Rethinking Model Scaling for Convolutional Neural Networks)
- 합성곱 신경망 기초 8(Data Augmentation, 데이터 증강)
ResNet
- ILSVRC 2015 우승 (3.6% Top 5 Error)한 모델이며 Deep Residual Learning 이라고도 부른다.
- 152개의 Layer 구조이며 8배 깊은 Layers를 가졌음에도 불구하고 실행 시간이 VGGNet보다 빠르다.
- 이 모델은 일반적인 레이어만 깊은 모델들과 비교했을 때 성능이 좋을 뿐만 아니라 학습 속도도 더 빠르다.
Introduction
- VGGNet 논문에서 CNN 의 레이어가 깊어질수록 성능이 더 좋다는 것을 확인할 수 있었다.
- 하지만 레이어가 너무 깊어지면 Vanishing/Exploding gradient, 그리고 degradation problem 크게 이 두 가지 문제점에 봉착한다.
- 우선 Vanishing/Exploding gradient 같은 경우에는 레이어 사이에 batchNorm 을 적용해주면 해결할 수 있다.
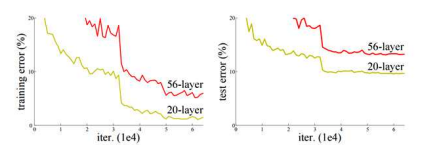
Degradation Problem 이란 정확도가 어느 순간부터 정체되고 레이어가 더 깊어질수록 성능이 더 나빠지는 현상을 의미한다.
이 논문에서는 Residual Learning 을 통해 Degradation Problem 을 해결하는 방법을 제시한다.
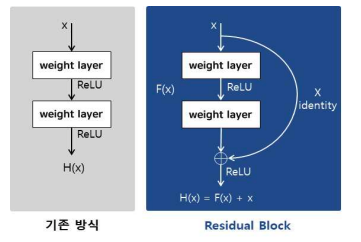
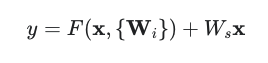
- 간단하게 input 을 x, input이 통과하는 Function 을 F(x), 그리고 Output 을 H(x) 이라고 가정해보자. F(x) = H(x) - x 를 최소화시키는 Residual mapping으로 H(x)를 재정의한다.
- Residual Learning 에서는 F(x) 를 H(x) - x 라고 define 해 주었다. 원래 Output H(x) 에서 자기 자신인 x 를 빼주기 때문에 ‘Residual Learning’ 이라는 이름을 가지게 된다.
- 또 x 가 이 F(x) 를 통과한 이후에, 이 값은 자기 자신인 x 와 더해주고, Layer를 Skip해서 더해주기에 ‘Skip Connections’ 이라고 부른다. 이 Residual Block 을 통과하고 나면 최종적인 값은 F(x) + x 가 나오게 된다.
- F(x) 와 x 를 직접적으로 더해주기 위해선 F(x) 와 x 가 서로 같은 Dimension 이어야 한다. 일반적으로 F(x) 와 이전의 input x가 채널수가 같다면 별다른 조치를 취해주지 않아도 그냥 더해주면 된다.
- 하지만 Channel 개수가 달라지거나 MaxPool 등에 의해서 x 의 크기가 달라질 때, padding 이나 별다른 Ws 를 곱해주어서 사이즈를 매칭 시켜주는 것이 중요하다.
ResNet Architecture
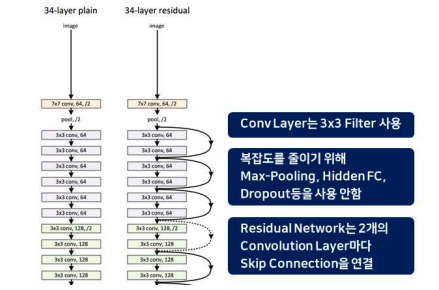
- ResNet 의 기본 구조는 VGGNet-34 을 따른다. 위 그림을 보면 VGG-34 과 모델 구성은 같은데, 레이어 두개마다 Skip Connection 을 해준다는 것을 볼 수 있다.
- 중간에 점선으로 표시된 Skip Connection 은 x 와 F(x) 의 Dimension 이 달라져서 따로 맞춰줘야 되는 Skip Connection 들을 의미한다.
Deeper Bottleneck Architectures
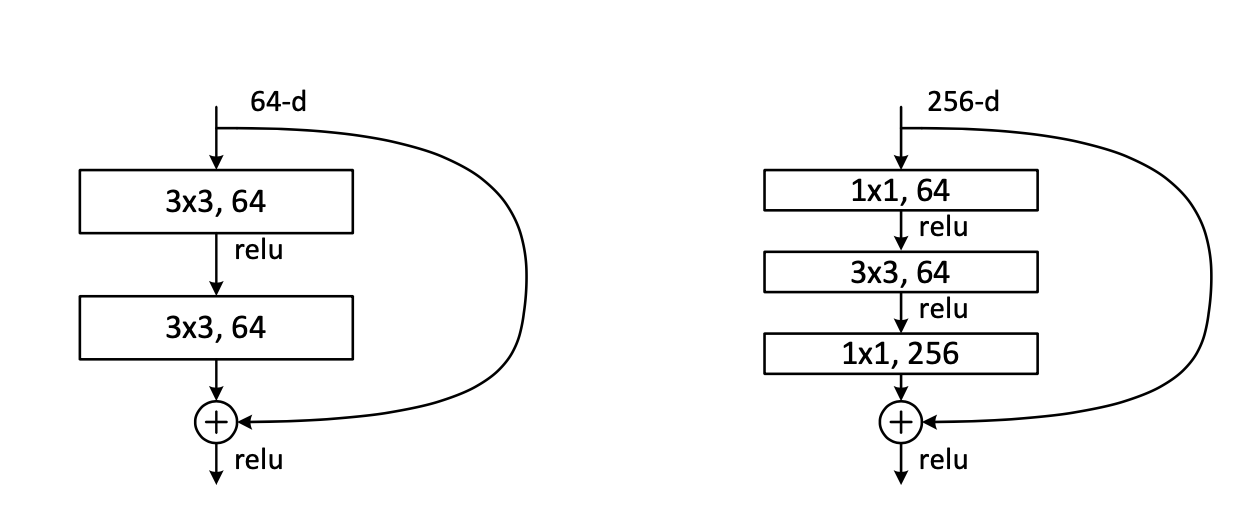
- 네트워크의 깊이가 50 을 넘어가면, 제아무리 ResNet을 이용하고 3x3 필터만 사용한다 할지라도 Training 시간이 매우 길어질 수 있다. 따라서 이 경우엔 원래 모델 구조에서 약간의 수정이 필요하다.
- 3x3 필터를 두 번 사용하는 대신, 1x1 -> 3x3 -> 1x1 필터들을 사용하는 구조를 만든다. 이렇게 수정한 구조는 Dimension 의 크기를 줄일 뿐만 아니라 시간 복잡도도 줄이는 효과를 볼 수 있다.
Experiments
ResNet 은 1000개의 클라스로 이루어진 ImageNet 2012 데이터셋으로 training
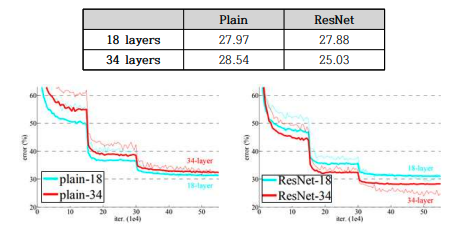
- 위 그래프에서 왼쪽 그림은 Plain Network 의 18, 34 Layer, 오른쪽 그림은 ResNet 의 18, 34 layer 의 Loss 과정이다.
- 우선 왼쪽 그림에서는 Degradation Problem 이 보이는 것을 확인할 수 있다. 34-Layer 네트워크가 18-layer 보다 Loss 가 높기 때문이다.
- 반면 ResNet 같은 경우엔 34-Layer 가 Loss 가 더 낮게 나오는 것을 확인할 수 있다. Degradation Problem 이 해결됐음을 보여주는 그래프이다.
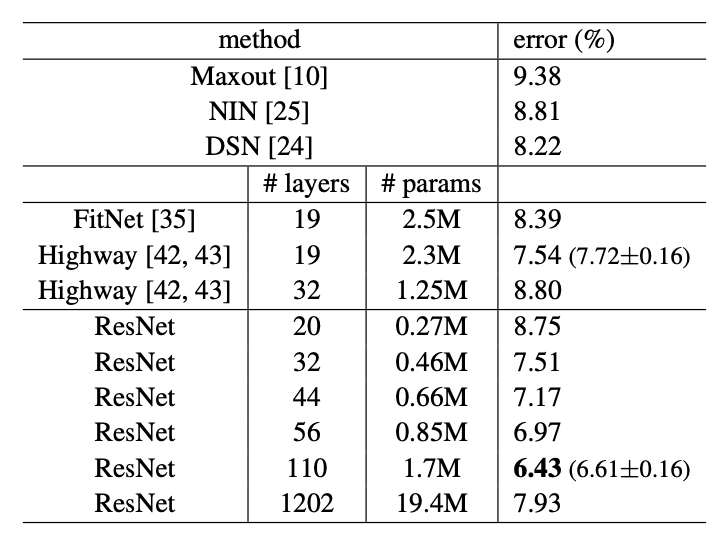
- 위 표에서는 더 깊은 ResNet 들의 성능을 보여준다. 레이어가 깊어지면 깊어질수록 error 는 줄어드는 경향성을 볼 수 있고, 110 개의 레이어가 있을 때 가장 적은 에러가 나온다.
- 하지만 그렇다고 너무 깊어지면, 예를 들어 1000 개 이상의 레이어가 존재할 때는 오버피팅으로 인하여 성능이 더 얕은 모델들보다 더 안 좋게 나온다.
참조 문헌
[1] He, K., Zhang, X., Ren, S., & Sun, J. (2016). Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 770-778).
https://www.cv-foundation.org/openaccess/content_cvpr_2016/papers/He_Deep_Residual_Learning_CVPR_2016_paper.pdf