CNN 강좌는 여러 절로 구성되어 있습니다.

• 합성곱 신경망 기초(CNN, Convolution Neural Network)
• 합성곱 신경망 기초 2(역전파, Backpropagation)
• 합성곱 신경망 기초 3(배치정규화, Batch Normalization)
• 합성곱 신경망 기초 4(가중치 초기화, Weight Initialization)
• 합성곱 신경망 기초 5(VGGNet, Very Deep Convolutional Network)
• 합성곱 신경망 기초 6(ResNet, Residual Learning for Image Recognition)
• 합성곱 신경망 기초 7(EfficientNet, Rethinking Model Scaling for Convolutional Neural Networks)
• 합성곱 신경망 기초 8(Data Augmentation, 데이터 증강)

배치 정규화

깊은 신경망일 수록 같은 Input 이라도 가중치가 조금이라도 다르다면 완전히 다른 결과를 가져올 수 있다.

“각 층이 활성화를 적당히 퍼뜨리도록 강제로 해보자”

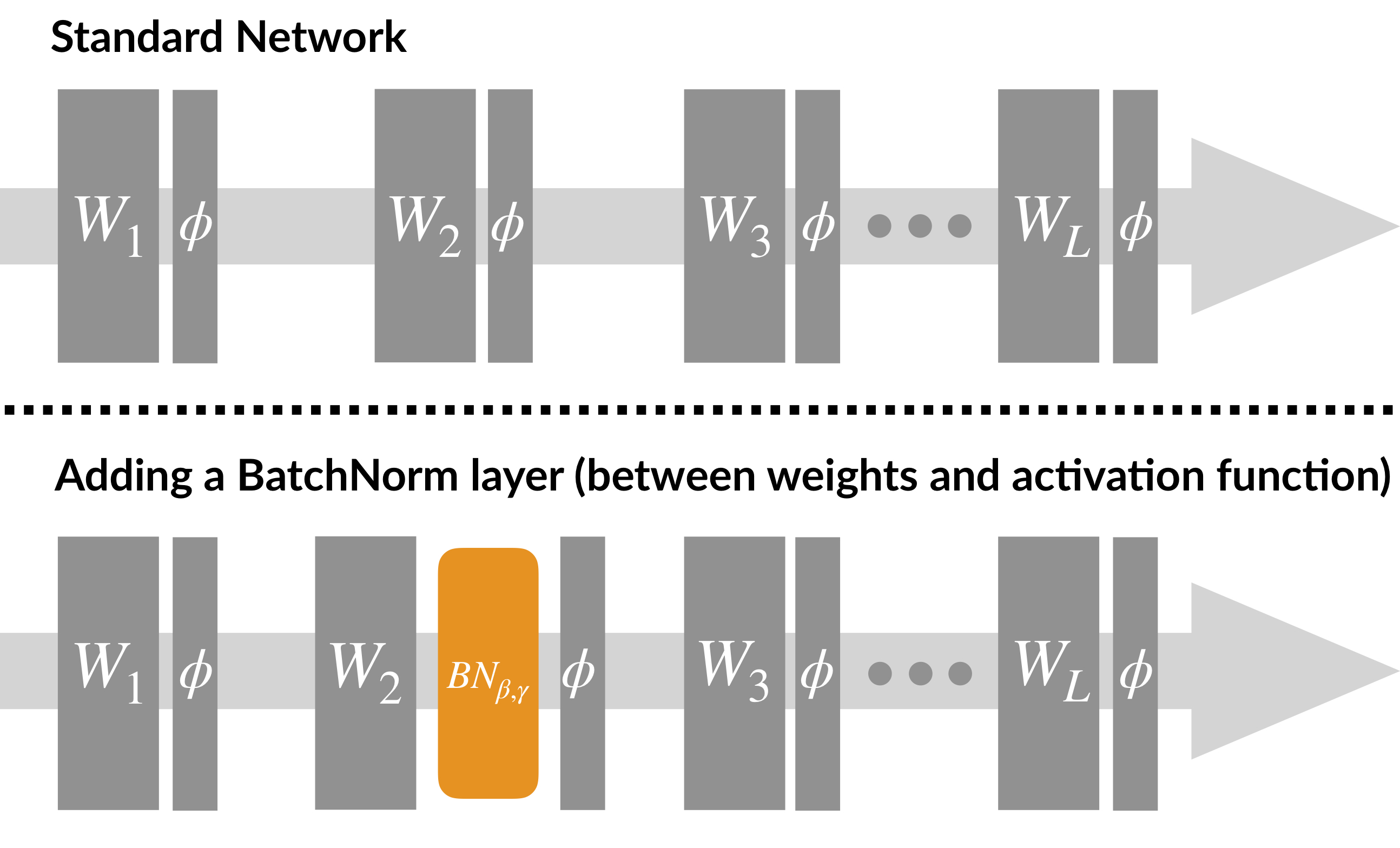
• 배치란? 신경망 학습시, 전체 데이터를 한 번에 학습시키지 않고, 조그만 단위로 분할해서 학습 시키는 것.
• 배치 정규화란? 배치 단위로 정규화 하는 것.

[배치 정규화 알고리즘]

• 엡실론은 분모가 0 이 되는 것을 막기 위한 아주 작은 숫자(1e-5~7)
• 정규화 이후, 배치 데이터들을 scale(감마(γ)), shift(베타(β)) 를 통해 새로운 값으로 바꾼다.
• 데이터를 계속 정규화 하게 되면, 활성화 함수의 비선형 성질을 잃게 되는 문제 발생

• 아래 그림과 같이 Sigmoid 함수 경우, 입력 값이 N(0, 1) 이라면, 95% 의 입력 값은 Sigmoid 함수 그래프의 중간 (x = (-1.96, 1.96) 구간)에 속하게 된다.

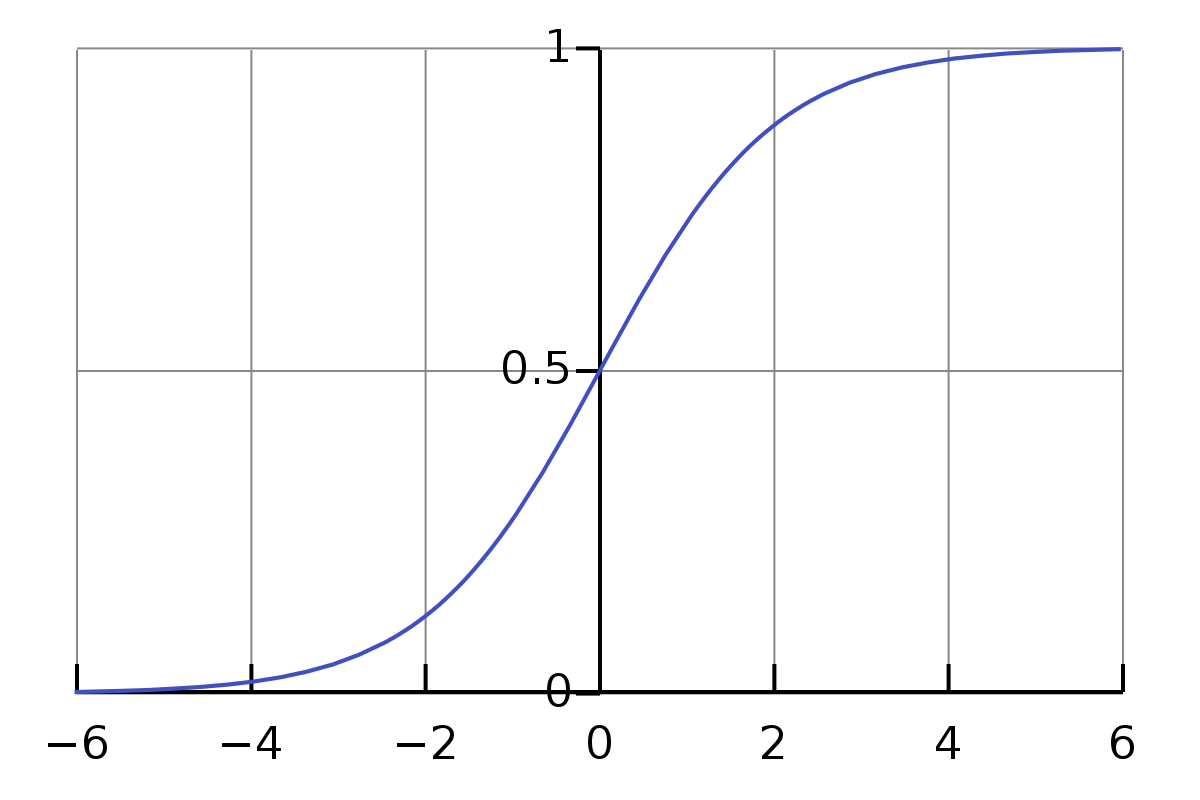
• 감마(γ), 베타(β)를 통해 활성함수로 들어가는 값의 범위를 변환하여 비선형 성질을 보존
• 감마(γ), 베타(β) 값은 학습 가능한 변수, 역전파를 통해서 학습

⭐배치 정규화 효과⭐

1. 학습이 빠르게 진행(Epoch 수를 줄이는데 효과적)
2. Dropout 필요성 감소
3. 더 높은 Learning rate 사용 가능
4. 규제 효과 (과적합 방지)
5. 그래디언트 손실(Vanishing Gradient)와 폭주(Exploding)문제 해결

---

참조 문헌 https://kharshit.github.io/blog/2018/12/28/why-batch-normalization https://reniew.github.io/13/
https://wooono.tistory.com/227